Laddering is a method for systematically exploring hierarchically organised knowledge. It was invented by Dennis Hinkle, in an unpublished PhD thesis, and developed further by various researchers, including Reynolds & Gutman, and Rugg & McGeorge.
The core concept uses a small set of questions to elicit knowledge systematically, moving up and down the hierarchies in which the knowledge is organised. For instance, you might use upward laddering to investigate people’s higher-level goals and values, or downward laddering to unpack layers of explanations of technical terms or subjective terms.
The core concept is simple, but using it properly involves understanding some basic graph theory and facet theory; otherwise, there is a risk of ending up with a tangled mess of apparently contradictory results.
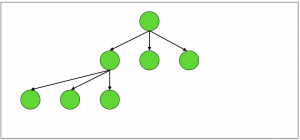
Laddering is designed to work with knowledge that is in a tree structure as opposed to a net structure, as shown in the diagram opposite. In a tree, the branches never re-join; in a net, branches may re-join.
Laddering is also designed to work with knowledge that is in the form of a directed graph, as opposed to an undirected graph, shown in the second diagram opposite. Directed graphs can be represented with arrows that show the direction; undirected graphs can be shown with simple lines, since the direction doesn’t matter in undirected graphs. For example, ‘parent’ relationships are directed; the sentence “X is the parent of Y” has a completely different meaning from “Y is the parent of X”. A corresponding example of an undirected graph would be that “Z is related to A” has the same meaning as “A is related to Z”.
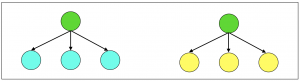
Laddering can also work with different facets within the same field, as in the third image opposite. For instance, you can ladder downwards from ‘car’ within the facet ‘types of car’ or within the facet ‘components of a car’. Each of these makes sense as long as you stay within the same facet (e.g. unpacking various types of car, and then sub-types of car).
Expert knowledge is often explicitly organised hierarchically in directed graphs; a lot of other knowledge can also be represented as directed graphs, such as explanations of subjective terms, or hierarchies of goals and values. These graphs are often large, involving dozens or hundreds of items, and multiple levels of hierarchy. The image opposite of a three layer graph shows one significant implication for laddering: it’s usually not practical to record a laddering session using a diagram in real time, since you can’t know in advance how many items you’ll need to fit in within a single layer. It’s much simpler to record the results as a series of small chunks, using a textual representation rather than a graphical one.
Forms of laddering that we find particularly useful are:
Downward laddering on explanations is useful for flushing out taken for granted knowledge and not worth mentioning knowledge, which typically emerge after two or more layers of explanation, and which would usually be missed by less rigorous methods.
It’s a powerful, elegant method; learning the basics doesn’t take long, and when you learn how to use it at an advanced level, it’s invaluable.
References
Reynolds, TJ & Gutman, J (1988). Laddering theory, method, analysis and interpretation, Journal of Advertising Research, 28, 1.
Rugg, G & McGeorge P (1995). Expert Systems, 12, 4.
A tree (left) versus a net (right)
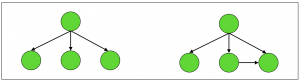
A directed graph (left) versus an undirected graph (right)

Two different facets for the same field; a blue facet (e.g. ‘type of’) and a yellow facet (e.g. ‘component of’)
Three layers within a graph